how to decide the final classification of Ligue 1 if it were to stop here?

DIn this coronavirus crisis, there are far more serious issues than stopping sports competitions. However, the indefinite pause of a large number of championships poses a big problem for their organizers: if the 2019-2020 season could not resume, how to decide the final ranking? The latter is not purely honorary. It conditions access to other competitions (European cups for example) and the amount of bonuses paid to participants (players or teams) depends on it.

Take the example of Ligue 1 football. A large number of matches in the 2019-2020 season have already been played (28 days out of 38, or more than 73%). If the championship ends there, how do you decide who wins, European Cup qualifiers and clubs relegated to Ligue 2 in the fairest way possible?

Jean-Michel Aulas, president of Olympique Lyonnais, who has had his worst season in Ligue 1 for over twenty years, jumped at the chance to defend the idea of ​​a season "White" : no winner, no relegated, and we will start next year in the European Cup with the same clubs as in 2019-2020.

This solution would suit OL's business well, which would thus participate in the 2020-2021 Champions League while its current ranking (7^e) gives him little hope of qualifying on the field. This solution would also be particularly unfair for the clubs that are doing well this season: Olympique de Marseille, Stade Rennais, but also Lorient and Lens, currently leading Ligue 2 and well placed to be promoted to Ligue 1 a year next.

The string is a little big. This proposition is sportingly and ethically indefensible. Since most of the championship has already been played, the results of the 279 games already played must be taken into account to determine the final ranking (March 7, Strasbourg-PSG, counting for the 28^e day had been postponed, already due to the coronavirus epidemic).

A simple solution would be to freeze the current classification, that is on the evening of the 27^e day, the evening of the 28^e, if Strasbourg-PSG could be played. However, is it really fair?

Imbalances in team calendars

The current classification is advantageous for certain teams: those which have so far only played once against PSG, which clearly dominates Ligue 1 and has won 22 of its 27 league matches; or those who have already played their two games (one at home, one away) against Toulouse, the easiest team to beat this year, red lantern with the meager total of 13 points and 3 wins in 28 games ; or those who have played more games at home than away (on the 28 days already played, some teams have played 13 games at home, others 14, others 15).

For example, Rennes, currently 3^e of the championship with 50 points, played only once against Paris (2-1 home victory in the 2^e day) while Lille, 4^e just one point from Rennes, has already played (and lost) its two games against PSG. These two teams, neck and neck for third place qualifying for the 2020-2021 Champions League, have already played their two games against Toulouse.

It is likely that, in hypothetical 37^e day, Lille would have won at home against Amiens while Rennes would have lost at the Parc des princes. We can for example measure the difficulty of the program remaining in Rennes and Lille by summing the points won so far by their future opponents: 347 for Lille, 379 for Rennes (and even 381 or 382 if we take Strasbourg-PSG account). Rennes therefore has a much more difficult program than Lille, and we can expect Rennes to gain fewer points than Lille in the last ten days.

However, Lille will have to play six of its last ten away games, against five for Rennes. From this point of view, the Rennes program is easier. What effect wins: the higher level of opponents or playing more games at home?

A method used for rankings of chess players

Mathematics solves these kinds of problems. I propose the following method, which is inspired by the method proposed by the physicist Arpad Elo in 1960 to classify chess players and used, among others, since 2003 to establish the FIFA classification of women's national teams, and since 2018 for that of men's teams.

However, unlike the Elo ranking, which takes into account all the history of matches, including those of past seasons, we want to only take into account the matches of the 2019-2020 season.

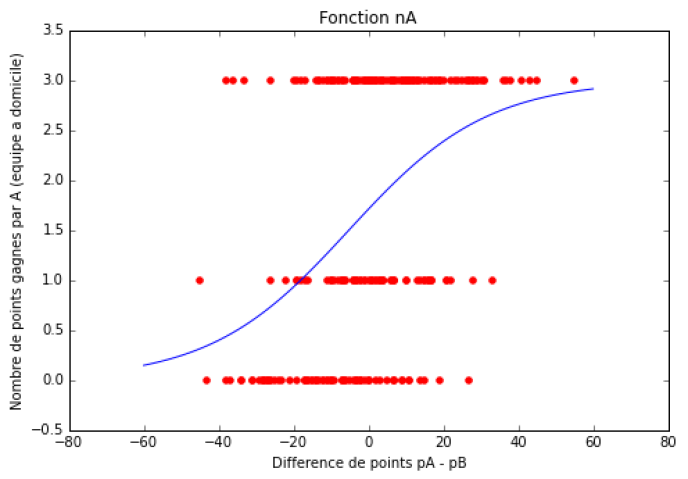
We will therefore assume that the average number of points nA won by team A when it plays at home against team B is a function of the difference pA – pB between the points won by A and B after 28 days of the League 1.

The greater the difference (for example pA – pB = 68 – 30 = 38 for PSG – Saint-Étienne on the program for the 33^e day), the larger nA is, close to 3 (3 points are allocated for a victory, 1 for a draw, 0 for a defeat).

The smaller the difference (pA – pB = 13 – 68 = -55 for Toulouse – PSG from 36^e day), the smaller nA is, close to 0.

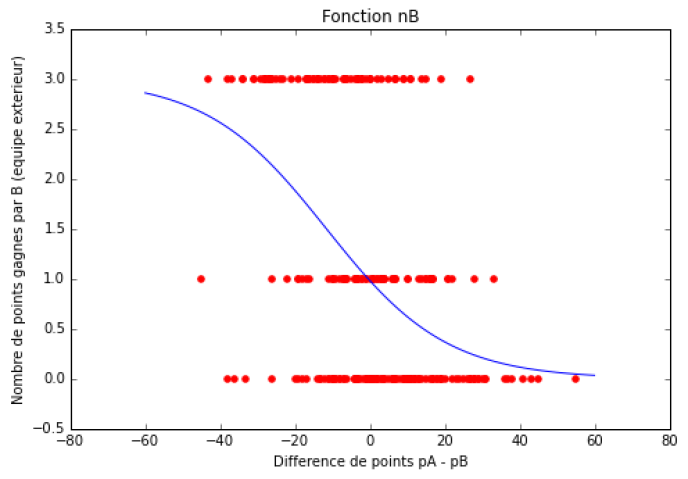
We also model nB, the average number of points won by team B (the visiting team), by a (other) function of pA – pB, this time decreasing.

When pA = pB, the two teams are of equal level, but nA is slightly larger than nB, due to the statistical advantage of playing at home.

We suggest choosing two so-called “sigmoid” functions, and for each of these two functions, two parameters (elasticity and “home advantage”) are calibrated based on the results of the 279 games already played.

For each team, we then add to the number of points already obtained the average number of points that would have been won during the last ten days, predicted by the functions nA and nB. We obtain the following classification:

Nothing provided for in the regulations in the event of force majeure

Rennes would therefore keep its 3^e square ; the first five places would remain unchanged, as would the last three. Montpellier (6^e) would gain two places, surpassing Nice which, unlike Montpellier, is very advantaged by the current classification: Nice has only played once against PSG, has already played twice against Toulouse and has already received 15 times out of 28.

There are of course finer models, bookmakers are fond of them. This has the merit of being simple while taking into account imbalances in the schedules of the teams. Of course it is only the expected number of points; if the season can come to an end, we can use these calculations to measure whether a team has done better or worse than expected.

It is surprising that Ligue 1, like apparently all of the major European football championships, has nothing in its regulations regarding these cases of force majeure.

Freeze the current ranking (with the problems we have described)? Keep the mid-season ranking? In mid-season all the teams played with each other exactly once, but only outside or only at home, and why not take into account the more recent results? Use a simple model like the one I proposed here?

The problem when deciding on an ex post rule is that you are open to criticism and suspicion of bias: whatever rule you choose will benefit some teams and disadvantage others.

Hence the importance of defining all the rules of the game before the start of the competition. To govern is to foresee, said Emile de Girardin.